ドップラー効果

ドップラー効果（ドップラーこうか、英: Doppler effect）またはドップラーシフト（英: Doppler shift）とは、音波や電磁波などの波の発生源（音源・光源など）が移動したりその観測者が移動することにより、波の発生源と観測者との間に相対的な速度が存在するときに、波の周波数が実際とは異なる値として観測される現象をいう。

概要

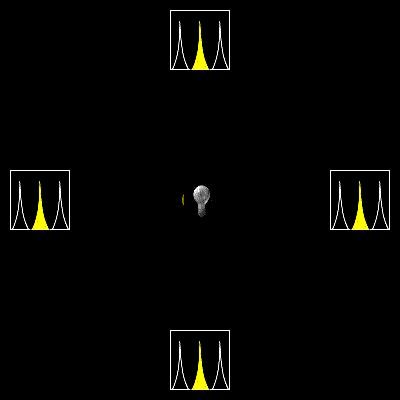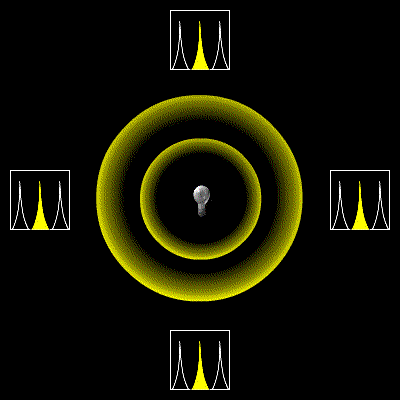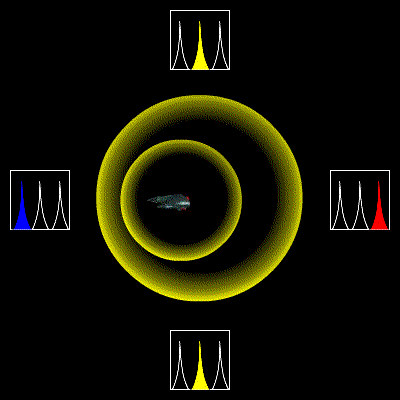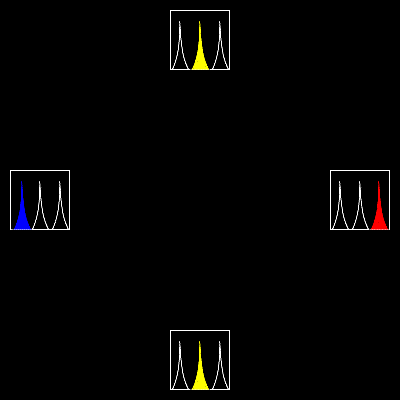
発生源が近付く場合には、波の振動が詰められて周波数が高くなり、逆に遠ざかる場合は振動が伸ばされて低くなる。有名な例としては、救急車が通り過ぎる際、近付くときにはサイレンの音が高く聞こえ、遠ざかるときには低く聞こえる。

音についてのこの現象は、古くから知られていたが、オーストリアの物理学者、クリスチャン・ドップラーが速度と周波数の間の数学的な関係式を1842年に見出し、オランダ人の化学者・気象学者であるクリストフ・ボイス・バロットが、1845年にオランダのユトレヒトで列車に乗ったトランペット奏者がGの音を吹き続け、それを絶対音感を持った音楽家が聞いて音程が変化することから証明を試みた。

観測者も音源も同一直線上を動き、音源S (Source) から観測者O (Observer) に向かう向きを正とすると、観測者に聞こえる音波の振動数は、

${\displaystyle f'=f\times {V-v_{\rm {o}} \over V-v_{\rm {s}}}}$

となる。ここで、${\displaystyle f}$ ： 音源の出す音波の振動数、${\displaystyle V}$ ： 音速、${\displaystyle v_{\rm {o}}}$ ： 観測者の動く速度、${\displaystyle v_{\rm {s}}}$ ： 音源の動く速度

上記の ${\displaystyle f'}$ を求める公式は右図の時空間モデルから導くことができる。

図の○は波の山、●は波の谷であり、音源は時刻 0 に原点を通るとしている。速度 ${\displaystyle v_{\rm {o}}}$ で原点から離れる観測者が聴く音の周期 ${\displaystyle T_{\rm {o}}}$ は山と山の間隔の t 軸への射影であり、図の赤い2つの三角形は相似である。

光のドップラー効果

光の場合でも同様の効果が観測され、遠ざかる光源からの光は赤っぽく見え（赤方偏移）、近付く光源からの光は青っぽく見える（青方偏移）。しかし、光の伝播は特殊相対性理論に従うため、通常の波のドップラー効果とは違った現象を見せる。

そもそもドップラー効果の原因は、波源や観測者が波の媒質に対して速度を持つために波の山の間隔が変わる所にあるが、光は波源や観測者の速度によらず常に光速 ${\displaystyle c}$ で伝播するように観測されるので、山の間隔の変わり方が通常の波の場合とは異なってくる。また、光の場合は波源が運動していると、特殊相対論的な効果によって波源上での時間の進み方が遅れて観測される。これにより、波源から出る光の振動数が小さく観測される効果が付け加わる。

以上の効果によって、光源Sが観測者Oから見て角度${\displaystyle \theta }$の方向に速さ ${\displaystyle V}$ で運動している場合、Oでの光の振動数 ${\displaystyle \nu '}$ は、

${\displaystyle \nu '=\nu \times {{\sqrt {1-(V/c)^{2}}} \over 1-(V/c)\cos \theta }}$

となる。ここで、${\displaystyle \nu }$ ： 光源の出す光の振動数、${\displaystyle V}$： 観測者から見た光源の速さ、${\displaystyle c}$ ： 光速、${\displaystyle \theta }$ ： 観測者から見た光源の動く方向（${\displaystyle \theta }$=0 ：観測者に向かってくる場合）

重要なのは、光の場合には光源が観測者の視線方向に対して垂直に運動しており、視線方向の速度を持っていない場合(${\displaystyle \theta }$=90°)でも光の振動数が変化して見えることである。これを横ドップラー効果という。

光のドップラー効果は星虹（スターボウ）として観測が可能であるという説がある。

実用

実際の活用法としては、恒星などの天体の可視光スペクトルに見られる吸収線（フラウンホーファー線）の波長の理論値とのズレ（ドップラー・シフト）から、地球とその天体との相対速度を算出できる。また、同じ電磁波におけるドップラー効果を利用したものとしてドップラー・レーダーがある。

原子炉のドップラー効果

原子炉の安定性にもドップラー効果は関係する。中性子の核反応スペクトルにも熱運動によるドップラー幅がある。温度が上がるとドップラー幅は広がり、その結果中性子の吸収が起きやすくなる。これは温度が上がるにつれて系内の中性子が少なくなることを意味し、そのため核分裂連鎖反応は収束する方向となる。すなわち、核分裂連鎖反応は温度に対して一定の自己制御性をもっている。原子炉においては、このことを指してドップラー効果と呼び、温度上昇に対する反応度の低下の割合をドップラー係数という。

ドップラー効果を応用した装置

• ロータリースピーカー - 上記効果など応用して音色を変化させるスピーカー。演奏時に使用される。
• ドップラー・レーダー
• 近接信管
• レーザドップラー流速計
• スピード測定器
• 医療用超音波検査装置
• ドップラー・ライダー
• 方向探知
• 測位衛星

脚注

参考文献

• Doppler, Christian Andreas、1842年『Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels』（Studnicka, Frantisek Josef 1903年 Königl. Böhm.科学出版社再版）、ウィキソース：de:Über das farbige Licht der Doppelsterne und einiger anderer Gestirne des Himmels、インターネットアーカイブ: ueberdasfarbigel00doppuoft.

関連項目

• 物理学 - 波動論
• フェージング